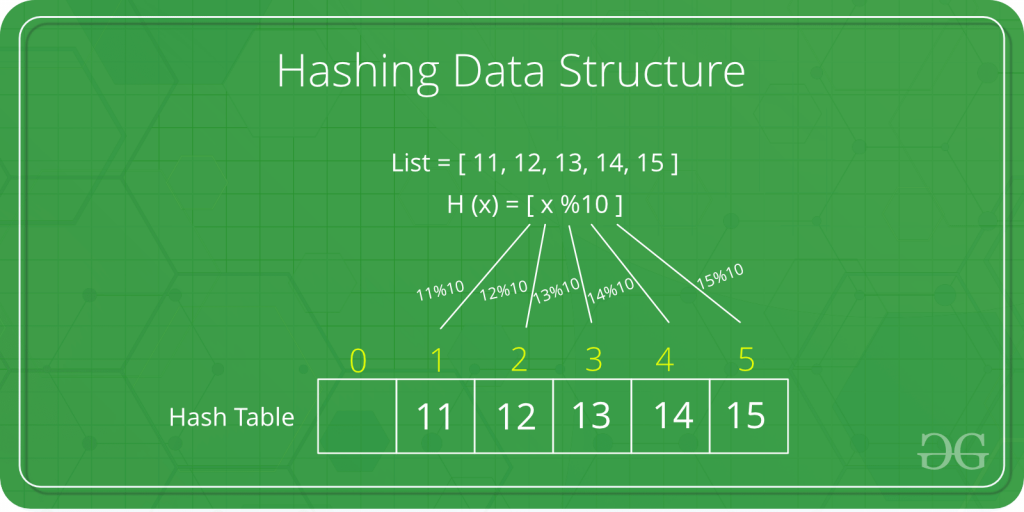
1. Hashing
Dapat diartikan sebagai aktivitas untuk mengubah suatu objek menjadi serangkaian angka/karakter/sejenisnya. Pada contoh sebelumnya, kita melakukan hash pada string menjadi bilangan.Anda mungkin menyadari bahwa tabel T pada contoh sebelumnya bekerja seperti array. Kita seakan-akan dapat melakukan operasi:
T["gozali"] = 3;
printf("%d\n", T["gozali"]);
Pada ilmu komputer, tabel seperti ini disebut sebagai hash table. Struktur data ini erat kaitannya dengan konsep "key value". Key adalah hal yang menjadi indeks, dan value adalah nilai yang berasosiasi dengannya. Pada contoh permasalahan sebelumnya, nama mahasiswa merupakan key, dan IPK merupakan value.
Fungsi Hashing
Pada bagian sebelumnya, saya memberi contoh fungsi hashing sederhana. Sebenarnya fungsi hashing itu bebas, terserah Anda ingin mendefinisikannya seperti apa. Namun, diharapkan fungsi hashing memiliki kriteria sebagai berikut:- Untuk dua buah key yang sama, hasil hashing-nya selalu sama.
- Memiliki kompleksitas rendah.
- Meminimalkan collision (akan dijelaskan pada bagian selanjutnya).
Hash Function
• Mid-square
• Division (most common)
• Folding
• Digit Extraction
• Rotating Hash
Hash Table adalah sebuah struktur data yang terdiri atas sebuah tabel dan fungsi yang bertujuan untuk memetakan nilai kunci yang unik untuk setiap record (baris) menjadi angka (hash) lokasi record tersebut dalam sebuah tabel.
Keunggulan dari struktur hash table ini adalah waktu aksesnya yang cukup cepat, jika record yang dicari langsung berada pada angka hash lokasi penyimpanannya. Akan tetapi pada kenyataannya sering sekali ditemukan hash table yang record-recordnya mempunyai angka hash yang sama (bertabrakan).
Pemetaan hash function yang digunakan bukanlah pemetaan satusatu, (antara dua record yang tidak sama dapat dibangkitkan angka hash yang sama) maka dapat terjadi bentrokan (collision) dalam penempatan suatu data record. Untuk mengatasi hal ini, maka perlu diterapkan kebijakan resolusi bentrokan (collision resolution policy) untuk menentukan lokasi record dalam tabel. Umumnya kebijakan resolusi bentrokan adalah dengan mencari lokasi tabel yang masih kosong pada lokasi setelah lokasi yang berbentrokan.
Operasi Pada Hash Tabel
Ø insert: diberikan sebuah key dan nilai, insert nilai dalam tabel
Ø find: diberikan sebuah key, temukan nilai yang berhubungan dengan key
Ø remove: diberikan sebuah key,temukan nilai yang berhubungan dengan key, kemudian hapus nilai tersebut
Ø getIterator: mengambalikan iterator,yang memeriksa nilai satu demi satu
Collision (Tabrakan)
Keterbatasan tabel hash menyebabkan ada dua angka yang jika dimasukkan ke dalam fungsi hash maka menghasilkan nilai yang sama. Hal ini disebut dengan collision.
contoh: Kita ingin memasukkan angka 6 dan 29.
Hash(6) = 6 % 23 = 6
Hash(29)= 29 % 23 = 6
Pertama-tama anggap tabel masih kosong. Pada saat angka 6 masuk akan ditempatkan pada posisi indeks 6, angka kedua 29 seharusnya ditempatkan di indeks 6 juga, namun karena indeks ke-6 sudah ditempati maka 29 tidak bisa ditempatkan di situ, di sinilah terjadi collision. Cara penanganannya bermacam-macam :
Collision Resolution Open Addressing
1. Linear Probing
Pada saat terjadi collision, maka akan mencari posisi yang kosong di bawah tempat terjadinya collision, jika masih penuh terus ke bawah, hingga ketemu tempat yang kosong. Jika tidak ada tempat yang kosong berarti HashTable sudah penuh. Contoh deklarasi program:
struct { ... } node;
node Table[M]; int Free;
/* insert K */
addr = Hash(K);
if (IsEmpty(addr)) Insert(K,addr);
else {
/* see if already stored */
test:
if (Table[addr].key == K) return;
else {
addr = Table[addr].link; goto test;}
/* find free cell */
Free = addr;
do { Free--; if (Free<0) Free=M-1; }
while (!IsEmpty(Free) && Free!=addr)
if (!IsEmpty(Free)) abort;
else {
Insert(K,Free); Table[addr].link = Free;}
}
2. Quadratic Probing
Penanganannya hampir sama dengan metode linear, hanya lompatannya tidak satu-satu, tetapi quadratic ( 12, 22, 32, 42, … )
3. Double Hashing
Pada saat terjadi collision, terdapat fungsi hash yang kedua untuk menentukan posisinya kembali.
Collision Resolution Chaining
Ø Tambahkan key and entry di manapun dalam list (lebih mudah dari depan)
Ø Kerugian:
- Overhead pada memory tinggi jika jumlah entry sedikit
Ø Keunggulan dibandingkan open addressing:
- Proses insert dan remove lebih sederhana
- Ukuran Array bukan batasan (tetapi harus tetap meminimalisir collision: buat ukuran tabel sesuai dengan jumlah key dan entry yang diharapkan)
#include<stdio.h>
#define size 7
int arr[size];
void init()
{
int i;
for(i = 0; i < size; i++)
arr[i] = -1;
}
void insert(int value)
{
int key = value % size;
if(arr[key] == -1)
{
arr[key] = value;
printf("%d dimasukkan ke arr[%d]\n", value, key);
}
else
{
printf("Collision : arr[%d] sudah ada %d!\n", key, arr[key]);
printf("Tidak dapat memasukkan %d\n", value);
}
}
void del(int value)
{
int key = value % size;
if(arr[key] == value)
arr[key] = -1;
else
printf("%d tidak ada dalam hash table\n",value);
}
void search(int value)
{
int key = value % size;
if(arr[key] == value)
printf("Ditemukan\n");
else
printf("Tidak ditemukan\n");
}
void print()
{
int i;
for(i = 0; i < size; i++)
printf("arr[%d] = %d\n",i,arr[i]);
}
int main()
{
init();
insert(10); //key = 10 % 7 ==> 3
insert(4); //key = 4 % 7 ==> 4
insert(2); //key = 2 % 7 ==> 2
insert(3); //key = 3 % 7 ==> 3 (collision)
printf("Hash table\n");
print();
printf("\n");
printf("Menghapus 4..\n");
del(4);
printf("Setelah penghapusan hash table\n");
print();
printf("\n");
printf("Menghapus 10..\n");
del(10);
printf("Setelah penghapusan hash table\n");
print();
printf("\n");
printf("Mencari 2..\n");
search(2);
printf("Mencari 10..\n");
search(10);
return 0;
}
Implementasi Hash pada Blockchain
Peran penting kriptografi dalam jaringan blockchain terus berkembang tiada hentinya. Salah satunya adalah proses perhitungan sebuah data secara konkret dan unik. Metode ini dikenal dengan Hash, mungkin anda tak asing dengan kode unik yang banyak ditemukan di Blockchain dan itulah salah satu contoh Hash.
Nilai berharga sebuah data saat ini berpotensi dibobol atau diketahui oleh orang lain. Salah satu teknik mengakalinya ialah dengan pemberian kode unik. Ibarat peran dari sidik jari elektronik (digital fingerprint) pada data digital punya Anda.
Data tersebut akan aman dan pastinya menjadi orisinalitas data dari orang lain. Hanya orang yang terkait berhak dan bisa masuk ke akses data tersebut. Saat ini beragam proses pengamanan data, mulai dari sidik jari, sidik mata, dan di sistem Blockchain menggunakan kode unik (Hash).
Pada sebuah penelitian mengatakan bahwa, butuh waktu 3,67 miliar tahun untuk bisa memecahkan sebuah kode dengan 10 karakter tanpa simbol. Asumsinya dengan waktu proses selama 10,45 jam setiap harinya menggunakan aplikasi tebak 1000 tebakan/detik.
Password atau kode unik di blockchain punya nilai karakter yang lebih panjang dan menggunakan kode unik. Pastinya proses peretesan dengan aplikasi tebak saat ini jelas sangat lama dan bahkan mustahil. Itulah yang menjadi alasan bahwa Hash sangat penting dan dinilai sangat aman.
Tak hanya itu saja, Hash mampu mengubah setiap data yang mengalami perubahan dengan nilai unik sendiri. Ini yang tidak didapatkan pada jaringan biasa. Selain itu, setiap data dokumen dengan panjang berapa pun akan menghasilkan nilai hash yang punya nilai panjang berbeda tergantung spesifikasi Hash yang digunakan.
Ada sejumlah hash yang digunakan saat ini. Fungsi dan keamanannya beragam dan dengan kemampuan transaksi data cepat. Apa sajakah sejumlah Hash tersebut, berikut ulasannya:
1. SHA256
Hash pertama sekali muncul dan digunakan di jaringan blockchain publik adalah SHA256. Hash ini digunakan pada Bitcoin khusus proses transaksi dan perhitungan nilai Hash. Pengguna ini sudah mulai dicetus sejak tahun 2001 oleh NIST (National Institute of Standard and Technology).

SHA256 merupakan generasi kedua dari hash jenis Sha, penggunaan angka 256 karena dasar data yang dihasilkan adalah 256 bit. SHA26 sendiri banyak digunakan oleh berbagai sistem blockchain lainnya karena punya kapasitas mengirim yang relatif kecil dan cepat. Apalagi untuk proses transaksi besar.
2. RIPEMD160
Hash RIPEMD160 merupakan singkat dari Race Integrity Primitive Evaluation Message Digest. Konsep dari algoritma dari hash ini dikembangkan oleh MD4. Jumlah data transaksi yang dihasilkan lebih kecil dibandingkan SHA256 yaitu hanya 160 bit.
Jelas ini lebih cepat dan bertenaga, sehingga mengurangi proses pending data. Peran utama yang diemban oleh RIPEMD160 adalah dengan membuat alamat Bitcoin yang diakumulasi berdasarkan pada kunci publik.
3. Beragam Hash pada Monero
Pada Monero, penerapan pada keamanan data menggunakan sejumlah Hash, mulai dari Keccak, Blake, Grostl, JH, dan Skein pada CryptoNote. Konsep dari Monero yang sangat kompleks seakan membuatnya dijuluki sebagai fully anonymous.
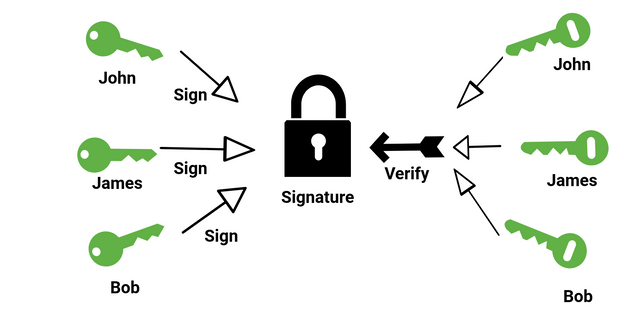
Monero menilai bahwa perlu adanya keamanan khusus dan beragam pada Hash. Inilah yang menjadi dasar lahirnya konsep CryptoNote. Pengguna yang mengirimkan transaksi atau data tidak dapat diidentifikasi oleh publik karena ada beberapa kunci tersebut. Ia kata sebagai pengalih dan membuat Anda sulit diintai dan data serta privasi tetap aman di jaringan Blockchain.
Pengertian Tree
Tree merupakan salah satu bentuk struktur data tidak linear yang menggambarkan hubungan yang bersifat hirarkis (hubungan one to many) antara elemen-elemen. Tree bisa didefinisikan sebagai kumpulan simpul/node dengan satu elemen khusus yang disebut Root dan node lainnya. Tree juga adalah suatu graph yang acyclic, simple, connected yang tidak mengandung loop.
Binary Tree
· Pengertian Binary Tree
Binary Tree merupakan salah satu bentuk struktur data tidak linear yang menggambarkanhubungan yang bersifat hirarkis (hubungan one to many) antara elemen-elemen. Tree bisa didefinisikan sebagai kumpulan simpul/node dengan satu elemen khusus yang disebut Root dan node lainnya ( disebut subtree).
Dalam tree terdapat jenis-jenis tree yang memiliki sifat khusus, diantaranya adalah binary tree.
Binary tree adalah suatu tree dengan syarat bahawa tiap node (simpul) hanya boleh memiliki maksimal dua subtree dan kedua subtree tersebut harus terpisah. Tiap node dalam binary treee boleh memiliki paling banyak dua child (anak simpul), secara khusus anaknya dinamakan kiri dan kanan.
Istilah pada pohon Binar
a. Pohon Biner Penuh (Full Binary Tree)
Semua simpul (kecuali daun) memiliki 2 anak dan tiap cabang memiliki panjang ruas yang sama.
b. Pohon Biner Lengkap (Complete Binary Tree)
Hampir sama dengan Pohon BinerPenuh, semua simpul (kecualidaun) memiliki 2 anak tetapi tiap cabang memiliki panjang ruas berbeda.
c. Pohon Biner Similer
Dua pohon yang memiliki struktur yang sama tetapi informasinya berbeda.
d. Pohon Biner Ekivalent
Dua pohon yang memiliki struktur dan informasi yangsama.
e. Pohon Biner Miring (Skewed Tree)
Dua pohon yang semua simpulnya mempunyai satu anak / turunan kecuali daun.
· Kunjungan pada pohon Biner
Kunjungan pohon biner terbagi menjadi 3 bentuk binary tree :
1. Kunjungan secara preorder ( Depth First Order), mempunyai urutan :
a. Cetak isi simpul yang dikunjungi ( simpul akar ),
b. Kunjungi cabang kiri,
c. Kunjungi cabang kanan .
2. Kunjungan secara inorder ( symetric order), mempunyai urutan :
a. Kunjungi cabang kiri,
a. Kunjungi cabang kiri,
b. Cetak isi simpul yang dikunjungi (simpul akar),
c. Kunjungi cabang kanan .
3. Kunjungan secara postorder, mempunyai urutan :
a. Kunjungi cabang kiri,
a. Kunjungi cabang kiri,
b. Kunjungi cabang kanan,
c. Cetak isi simpul yang dikunjungi ( simpul akar ).
· Aplikasi pohon Biner
Notasi Prefix, Infix dan Postfix
Pada bagian ini akan dibahas tentang bagaimana menyusun sebuah Pohon Binar yang apabila dikunjungi secara PreOrder akan menghasilkan Notasi Prefix,kunjungan secara InOrder menghasilkan Notasi Infix, dankunjungan PostOrder menghasilkan Notasi Postfix.
Contoh program Binary Tree
#include<stdio.h>
struct bin_tree {
int data;
struct bin_tree * right, * left;
};
typedef struct bin_tree node;
void insert(node ** tree, int val)
{
node *temp = NULL;
if(!(*tree))
{
temp = (node *)malloc(sizeof(node));
temp->left = temp->right = NULL;
temp->data = val;
*tree = temp;
return;
}
if(val < (*tree)->data)
{
insert(&(*tree)->left, val);
}
else if(val > (*tree)->data)
{
insert(&(*tree)->right, val);
}
}
void print_preorder(node * tree)
{
if (tree)
{
printf("%d\n",tree->data);
print_preorder(tree->left);
print_preorder(tree->right);
}
}
void print_inorder(node * tree)
{
if (tree)
{
print_inorder(tree->left);
printf("%d\n",tree->data);
print_inorder(tree->right);
}
}
void print_postorder(node * tree)
{
if (tree)
{
print_postorder(tree->left);
print_postorder(tree->right);
printf("%d\n",tree->data);
}
}
void deltree(node * tree)
{
if (tree)
{
deltree(tree->left);
deltree(tree->right);
free(tree);
}
}
node* search(node ** tree, int val)
{
if(!(*tree))
{
return NULL;
}
if(val < (*tree)->data)
{
search(&((*tree)->left), val);
}
else if(val > (*tree)->data)
{
search(&((*tree)->right), val);
}
else if(val == (*tree)->data)
{
return *tree;
}
}
int main()
{
node *root;
node *tmp;
node *temp;
node *tempo;
node *temps;
root = NULL;
insert(&root, 39);
insert(&root, 54);
insert(&root, 27);
insert(&root, 76);
insert(&root, 22);
insert(&root, 17);
insert(&root, 62);
printf("Pre Order\n");
print_preorder(root);
printf("In Order\n");
print_inorder(root);
printf("Post Order\n");
print_postorder(root);
tmp = search(&root, 27);
if (tmp)
{
printf("node = %d\n", tmp->data);
}
else
{
printf("Data tidak dapat ditemukan.\n");
}
temp = search(&root, 100);
if (temp)
{
printf("node = %d\n", temp->data);
}
else
{
printf("Data tidak dapat ditemukan.\n");
}
tempo = search(&root, 22);
if (tempo)
{
printf("node = %d\n", tempo->data);
}
else
{
printf("Data tidak dapat ditemukan.\n");
}
temps = search(&root, 45);
if (temps)
{
printf("node = %d\n", temps->data);
}
else
{
printf("Data tidak dapat ditemukan.\n");
}
deltree(root);
}
Comments
Post a Comment