Final Review

Cathleen 2301867910

AVL Tree

Dalam Binary Search Tree, tinggi maksimal suatu tree adalah N-1,

dimana N adalah jumlah node. Dalam melakukan suatu operasi, 

Dengan Balanced Binary Search Tree, kita dapat membuat suatu tree dengan tinggi minimum.
untuk menetapkan tingginya, kita dapat menggunakan rumus berikut:

O(log n)

AVL Tree adalah Binary Search Tree yang memiliki perbedaan tinggi/ level maksimal 1 antara subtree kiri dan subtree kanan. AVL Tree muncul untuk menyeimbangkan Binary Search Tree. Dengan AVL Tree, waktu pencarian dan bentuk tree dapat dipersingkat dan disederhanakan.

Insertion

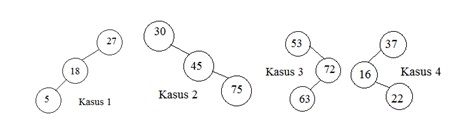
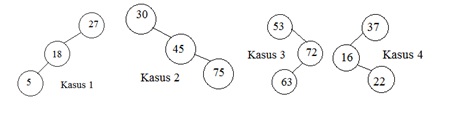
Ada 4 kasus yang biasanya terjadi saat operasi insert dilakukan, yaitu :
anggap T adalah node yang harus diseimbangkan kembali
– Kasus 1 : node terdalam terletak pada subtree kiri dari anak kiri T (left-left)
– Kasus 2 : node terdalam terletak pada subtree kanan dari anak kanan T (right-right)
– Kasus 3 : node terdalam terletak pada subtree kanan dari anak kiri T (right-left)
– Kasus 4 : node terdalam terletak pada subtree kiri dari anak kanan T (left-right)

Ke-4 kasus tersebut dapat diselesaikan dengan melakukan rotasi
– Kasus 1 dan 2 dengan single rotation
– Kasus 3 dan 4 dengan double rotation

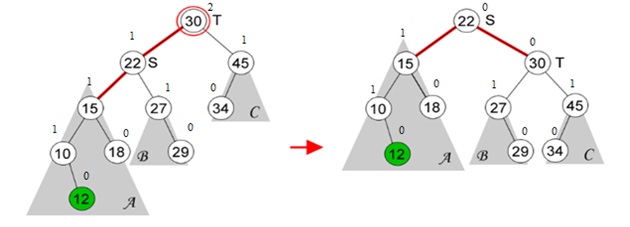
Contoh – Single Rotation: Jika suatu Tree diinsert node baru dengan nilai 12, maka akan terjadi ketidak seimbangan dan hal ini terletak pada posisi root

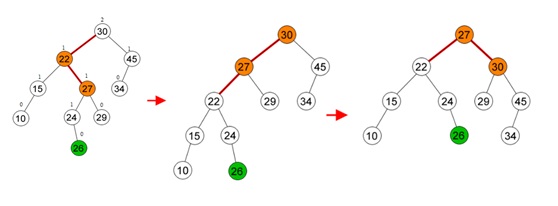
Contoh – Double Rotation : Jika terdapat sebuah tree yang kemudian dilakukan insert node 26. Maka akan terjadi ketidak seimbangan, sehingga terlihat dari bentuknya dapat diselesaikan dengan kasus 4.

Deletion

Ada 2 kasus yang biasanya terjadi saat operasi delete dilakukan, yaitu :
– Jika node yang akan dihapus berada pada posisi leaf atau node tanpa anak, maka dapat langsung di hapus.

• Jika node yang akan dihapus memiliki anak, maka proses penghapusannya harus di cek kembali untuk menyeimbangkan Binary Search Tree dengan perbedaan tinggi / level maksimal 1.
• anggap T adalah node yang harus diseimbangkan kembali
  – Kasus 1 : node terdalam terletak pada subtree kiri dari anak kiri T (left-left)
  – Kasus 2 : node terdalam terletak pada subtree kanan dari anak kanan T (right-right)
  – Kasus 3 : node terdalam terletak pada subtree kanan dari anak kiri T (right-left)
  – Kasus 4 : node terdalam terletak pada subtree kiri dari anak kanan T (left-right)
  

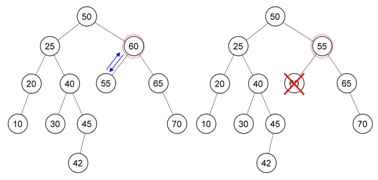
Berikut contoh dalam menghapus node AVL Tree, terdapat AVL Tree yang kemudian di hapus node 60. Dengan gambaran sebagai berikut :

Yang akan menggantikan posisi node 60 adalah node 55. Akan terjadi ketidak seimbangan. Dengan tampilan sebagai berikut :

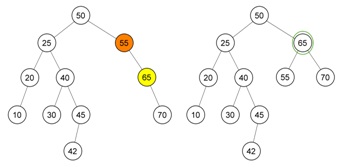
Maka akan dilakukan single rotation pada node 55 dengan kasus ketidak seimbangan pada kasus no. 2. Dengan tampilan setelah dilakukan single rotation sebagai berikut :

Ketika sudah dilakukan single rotation dan dilakukan kembali perbedaan tinggi / level maksimal 1 ternyata terdapat ketidak seimbangan yang terjadi. Sehingga diperlukan double rotation dengan kasus no. 4. Sehingga hasil dari rotasi yang dilakukan adalah sebagai berikut :

Contoh kodingan AVL Tree:

#include<stdio.h>
#include<stdlib.h>

struct bst{
int key;
int height;
bst* left;
bst* right;
};

bst* new_node(int key){
bst* curr = new bst;
curr->key = key;
curr->left = curr->right = NULL;
curr->height = 1;

return curr;
}

int max(int a, int b){
if(a > b){
return a;
}

else{
return b;
}

}

int getHeight(bst* root){
if(root == NULL){
return 0;
}

return root->height;
}

int getBalance(bst* root){
if(root == NULL){
return 0;
}

return getHeight(root->left) - getHeight(root->right);
}

bst* successor(bst* data){
bst* curr = data;

while(curr->left != NULL){
curr = curr->left;
}

return curr;
}

bst* leftRotate(bst* x){
bst* y = x->right;
bst* z = y->left;

y->left = x;
x->right = z;

x->height = max(getHeight(x->left), getHeight(x->right)) + 1;
y->height = max(getHeight(y->left), getHeight(y->right)) + 1;

return y;
}

bst* rightRotate(bst* x){
bst* y = x->left;
bst* z = y->right;

y->right = x;
x->left = z;

y->height = max(getHeight(y->left), getHeight(y->right)) + 1;
x->height = max(getHeight(x->left), getHeight(x->right)) + 1;

return y;
}

bst* balance(bst* root){
root->height = 1 + max(getHeight(root->left), getHeight(root->right));

int balance = getBalance(root);

if(balance > 1 && getBalance(root->left) >= 0){
return rightRotate(root);
}

else if(balance < -1 && getBalance(root->right) <= 0){
return leftRotate(root);
}

else if(balance > 1 && getBalance(root->left) < 0){
root->left = leftRotate(root->left);

return rightRotate(root);
}

else if (balance < -1 && getBalance(root->right) > 0){
root->right = rightRotate(root->right);

return leftRotate(root);
}

return root;
}

bst* insert(bst* root, int key){
if(!root){
return new_node(key);
}

if(key > root->key){
root->right = insert(root->right, key);
}

else if(key < root->key){
root->left = insert(root->left, key);
}

else{
return root;
}

return balance(root);
}

void preorder(bst* root){
if(root){
printf("%d\n", root->key);
preorder(root->left);
preorder(root->right);
}
}

void postorder(bst* root){
if(root){
postorder(root->left);
postorder(root->right);
printf("%d\n", root->key);
}
}

void inorder(bst* root){
if(root){
inorder(root->left);
printf("%d\n", root->key);
inorder(root->right);
}
}

bst* Delete(bst* root, int key){
if(!root){
return root;
}

if(key > root->key){
root->right = Delete(root->right, key);

}

else if(key < root->key){
root->left = Delete(root->left, key);
}

else{
if(root->left && !root->right){
bst* child = root->left;
*root = *child;
free(child);
}

else if(!root->left && root->right){
bst* child = root->right;
*root = *child;
free(child);
}

else if(!root->left && !root->right){
root == NULL;
free(root);
}

else{
bst *replace = successor(root->right);
root->key = replace->key; 
root->right = Delete(root->right, replace->key); 
}
}

if(!root){
return root;
}

return balance(root);
}

int main(){
bst* root = NULL;

root = insert(root, 10); 
root = insert(root, 20); 
root = insert(root, 30); 
root = insert(root, 40); 
root = insert(root, 50); 
root = insert(root, 25); 

root = Delete(root, 40);

postorder(root);
return 0;
}

Heaps & Tries

Heap

Struktur data heap adalah sebuah objek array yang dapat dengan mudah divisualisasikan sebagai complete tree. Ada korespondensi satu ke satu diantara elemen array dan node dari tree. tree itu benar-benar penuh pada semua tingkatan kecuali mungkin yang terendah, yang diisi dari kiri sampai titik tertentu. Semua node dari heap juga memenuhi hubungan bahwa nilai kunci pada setiap node pada kurangnya sama besar dengan nilai pada anak-anaknya.

Ini dapat dilihat sebagai sebuah pohon biner dengan dua kendala tambahan:

1. Bentuk property : pohon itu adalah complete binary tree , yaitu semua tingkat tree, kecuali mungkin yang terakhir (paling dalam) sepenuhnya diisi, dan, jika tingkat terakhir tree itu tidak lengkap, maka node pada tingkat itu diisi dari kiri ke kanan.
2. Sifat heap: setiap node lebih besar dari atau sama dengan masing-masing anak sesuai dengan perbandingan predikat yang ditetapkan untuk struktur data.

Jenis heap :
Min Heap: setiap elemen node adalah lebih kecil daripada children nya. Ini menunjukan bahwa elemen terkecil terletak pada root dari tree. Unsur terbesar adalah terletak di suatu tempat di salah satu node leaves.

Max Heap: setiap elemen node adalah lebih besar daripada children nya.Karena urutan sibling dalam heap tidak ditentukan oleh sifat heap, dua node tunggal anak-anak bisa secara bebas dipertukarkan kecuali melakukan hal itu melanggar properti bentuk Heap operations

Insert
Untuk menambahkan sebuah element ke HEAP kita harus melakukan operasi up-heap (juga dikenal sebagai bubble-up, percolate-up, sift-up, heapify-up, atau cascade-up) untuk mengembalikan sifat heap. Kita dapat melakukan ini dalam O (log n) time, menggunakan binary heap, dengan mengikuti algoritma ini:

1. Tambahkan elemen pada level bawah heap.
2. Bandingkan elemen yg baru ditambahkan dengan parentnya, jika mereka berada di urutan yang benar, berhenti.
3. Jika tidak, swap elemen dengan parent dan kembali ke langkah sebelumnya.
   Kita melakukan ini maksimum sekali untuk masing-masing tingkat di ketinggian tree, yang adalah O (log n). Namun, karena sekitar 50% dari elemen adalah leaves dan 75% berada di dua level di bawah, kemungkinan bahwa unsur baru yang akan dimasukkan hanya akan berpindah beberapa level ke atas untuk mempertahankan heap. Dengan demikian, binary heap mendukung insertion rata-rata dalam waktu yang konsta, O (1).

Misalkan kita memiliki heap

dan kita ingin menambahkan nomor 15 ke heap. Pertama-tama kita tempatkan 15 di posisi yg ditandai dengan X. Namun, sifat heap dilanggar karena 15 lebih besar dari 8, jadi kita perlu menukar 15 dan 8. Jadi, kita memiliki heap yg tampak sebagai berikut setelah swap pertama:

Namun sifat heap masih dilanggar karena 15 lebih besar dari 11, jadi kita perlu swap lagi:

Ini adalah max-heap yang valid. Tidak perlu untuk memeriksa children setelah ini. Sebelum kita menempatkan 15 pada X, tumpukan ini valid, yang berarti 11 lebih besar dari 5. Jika 15 lebih besar dari 11, dan 11 lebih besar dari 5, maka 15 harus lebih besar dari 5, karena dari relasi transitif.

remove
Prosedur untuk men-delete akar dari tumpukan dan restorasi disebut down-heap (juga dikenal sebagai bubble-down, percolate-down, sift-down, heapify-down, or cascade-down) Ganti root heap dengan elemen terakhir pada level terakhir. Bandingkan root baru dengan childrennya, jika mereka berada di urutan yang benar, berhenti. Jika tidak, swap unsur dengan salah satu childrennya dan kembali ke langkah sebelumnya. (Swap dengan children yang lebih kecil di min-heap dan children yang lebih besar di max-heap.)

Jadi, jika kita memiliki max heap-sama seperti sebelumnya, kita menghapus 11 dan menggantinya dengan 4.

Sekarang sifat heap dilanggar karena 8 lebih besar dari 4. Dalam hal ini, menukar dua elemen 4 dan 8, sudah cukup untuk mengembalikan sifat heap dan kita tidak perlu swap elemen lebih lanjut:

 

Kodingan:

#include <stdio.h>

#include <string.h>

#include <stdlib.h>

int arr[100], n;

void display(){

    int i;

    

    if (n == 0)

    {

        printf("\nHeap is empty\n");

        return;

    }

    for (i = 0; i < n; i++)

        printf("%d ", arr[i]);

    printf("\n");

}

void insert(int num, int loc){

    int parent;

    

    while (loc > 0){

        parent = (loc - 1)/2;

        

        if (num <= arr[parent]){

            arr[loc] = num;

            return;

        }

        

        arr[loc] = arr[parent];

        loc = parent;

    }

    

    arr[0] = num; 

}

void Delete(int num){

    int left, right, i, temp, parent;

    for (i = 0; i < num; i++){

        if (num == arr[i])

            break;

    }

    

    if (num != arr[i]){

        printf("\n%d not found in heap list\n", num);

        return;

    }

    

    arr[i] = arr[n - 1];

    n = n - 1;

    parent =(i - 1) / 2; 

    

    if (arr[i] > arr[parent]){

        insert(arr[i], i);

        return;

    }

    

    left = 2 * i + 1; 

    right = 2 * i + 2; 

    

while (right < n) {

        if (arr[i] >= arr[left] && arr[i] >= arr[right])

            return;

            

        if (arr[right] <= arr[left]){

            temp = arr[i];

            arr[i] = arr[left];

            arr[left] = temp;

            i = left;

        }

        

        else{

            temp = arr[i];

            arr[i] = arr[right];

            arr[right] = temp;

            i = right;

        }

        

        left = 2 * i + 1;

        right = 2 * i + 2;

    }

    if (left == n - 1 && arr[i])    {

        temp = arr[i];

        arr[i] = arr[left];

        arr[left] = temp;

    }

}

int main()

{

    int input, num;

    n = 0;

    

    do{

        printf("\n1. Insertion\n");

        printf("2. Deletion\n");

        printf("3. Display all elements\n");

        printf("4. Close\n\n");

        printf("Input : ");

        scanf("%d", &input);

        

        switch(input){

        case 1:

         system("cls");

            printf("Insert: ");

            scanf("%d", &num);

            insert(num, n);

            n = n + 1;

            display();

            break;

            

        case 2:

         system("cls");

            printf("Delete: ");

            scanf("%d", &num);

            Delete(num);

            display();

            break;

            

        case 3:

         system("cls");

            display();

            break;

            

        case 4:

         system("cls");

         printf("Thank you!");

            break;

    }

}while(input < 4);

}

 Tries

Tries atau prefix tree adalah suatu pohon struktur data yang terurut yang menyimpan data array, biasanya string. Kata tries diambil dari kata RETRIEVAL, karena tries dapat menemukan kata tunggal dalam kamus dengan hanya awalan katanya saja.

Tries sudah diterapkan ke banyak hal dalam kehidupan sehari-hari, contohnya pada web browser. suatu web browser dapat mengira atau mensugestikan kata-kata yang mungkin kita maksud saat kita mengetik huruf pertamanya saja. (autocomplete)

kemudian selain itu juga pada spell checker, spell checker dapat mengetahui spelling kata yang tepat saat kita melakukan kesalahan dalam pengetikan. (autocorrect)

Tries adalah suatu tree dimana setiap vertex/pathnya menggambarkan suatu kata, rootnya kosong

gambarannya :

gambar tersebut menunjukan kata : ALGO, API, BOM, BOS, BOSAN, BOR